
Loss function loss = np.multiply(np.log(predY), Y) + np.multiply((1 - Y), np.log(1 - predY)) #cross entropyĬost = -np.sum(loss)/m #num of examples in batch is m So, to illustrate the concept of the binary cross-entropy loss above, let’s define a small toy dataset consisting of five training examples.In order to make the case simple and intuitive, I will using binary (0 and 1) classification for illustration.
CROSS ENTROPY LOSS FUNCTION CODE
This often helps me understand things better, making the code easier to debug (for me). Personally, when I try to implement a new concept, I often opt for naive implementations before optimizing things, for example, using linear algebra concepts. This will allow us to implement the logistic loss (which we will call binary cross-entropy from now on) from scratch by using a Python for-loop (for the sum) and if-else statements. We have a likelihood function \(\mathcal\right)=(1-1)=0\). And maximizing accuracy serves the same goal as minimizing the error. If this sounds confusing, think about the classification accuracy and error. So, to find the optimal parameters, we can maximize the log-likelihood, or we can minimize the negative log-likelihood. This turns the maximization problem (maximizing the log-likelihood) into a minimization problem (minimizing the negative log-likelihood). (Since the log function is a monotonically increasing function, the parameters that maximize the likelihood also maximize the log-likelihood.) Also, we like to multiply the log-likelihood by (\(-1\)) such that it becomes a negative log-likelihood. Due to numeric advantages, we usually apply a log transformation to the likelihood function. In particular, we are given a data sample, and we want to find the parameters of a model that maximize the likelihood function. In statistics, we often talk about the concept of maximum likelihood estimation, which is an approach for estimating the parameters of a probability distribution or model. Here binary means that the classification problem has only two unique class labels (for example, email spam classification with the two possible labels spam and not spam).īinary classification and the logistic loss function # To understand the relationship between those and see how these concepts connect, let’s take a step back and start with a binary classification problem. Conceptually, the negative-log likelihood and the cross-entropy losses are the same. The quiz in the previous section introduced two losses, the NLLLoss (short for negative log-likelihood loss) and the CrossEntropyLoss.

However, if you are unsure, I encourage you to continue reading.
If you are confident about your answers and can explain them, you probably don’t need to read the rest of the article. (Note that NLLLoss is short for negative log-likelihood loss.)

(a) (nn.Softmax()) & (b) nn.CrossEntropyLoss().Next, let’s repeat this game considering a multiclass setting, like classifying nine different handwritten digits in MNIST. Question 2: Which of these options is/are acceptable but not ideal? Question 1: Which of the six options above is the best approach? (Note that BCELoss is short for binary-cross entropy loss.) (a) nn.LogSigmoid & (b) nn.BCEWithLogitsLoss() (a) nn.Sigmoid & (b) nn.BCEWithLogitsLoss() If you are interested in a binary classification task (e.g., predicting whether an email is spam or not), these are some of the options you may choose from: Oh no, two essential parts are missing! Now, there are several options to fill in the missing code for the boxes (a) and (b), where blank means that no additional code is required. Assume we are interested in implementing a deep neural network classifier in PyTorch. Let’s start this article with a little quiz. (And yes, when I am not careful, I sometimes make this mistake, too.) So, in this article, let me tell you a bit about deep learning jargon, improving numerical performance, and what could go wrong.
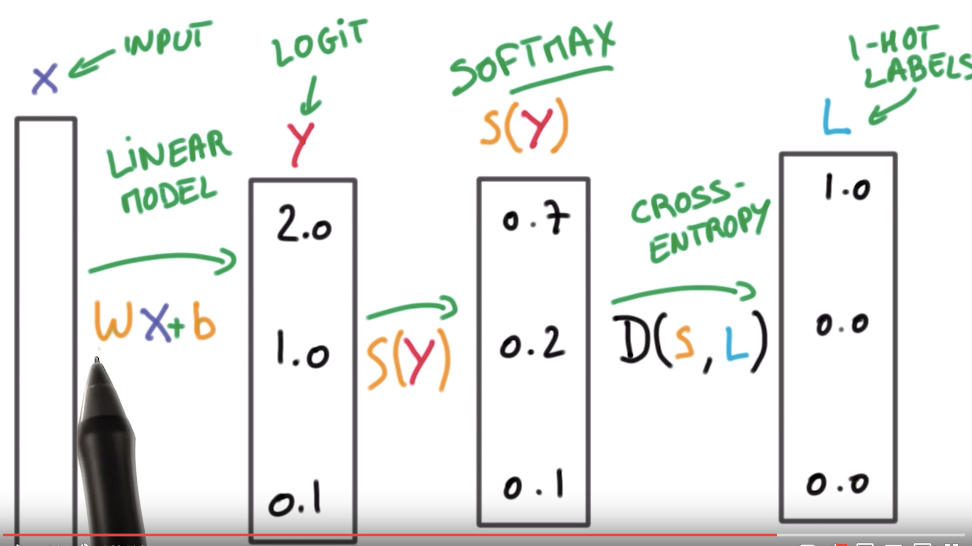
We can compute the cross-entropy loss in one line of code, but there’s a common gotcha due to numerical optimizations under the hood. You may wonder why bother writing this article computing the cross-entropy loss should be relatively straightforward!? Yes and no. There are two parts to it, and here we will look at a binary classification context first. In this article, I am giving you a quick tour of how we usually compute the cross-entropy loss and how we compute it in PyTorch. The cross-entropy loss is our go-to loss for training deep learning-based classifiers.


 0 kommentar(er)
0 kommentar(er)
